Based on the Chapter written by Prof. Dr. Jan K. Kruger:
"Brillouin Spectroscopy and its Application to Polymers"
Appeared in the book: Optical Techniques to Characterize Polymer Systems (Edited by Heinz Bässler) Elsevier 1989
BRIEF INTRODUCTION TO CLASSICAL BRILLOUIN SPECTROSCOPY ...
Brillouin spectroscopy (BS) applied to polymers primarily concerns inelastic light scattering on thermally excited sound waves (phonons) at hypersonic frequencies (~10 MHz to ~100 GHz). The Brillouin scattering effect was predicted first by Brillouin [1] and Mandelshtam [2] and for the first time experimentally verified by Gross [3]. The kinematics of this light scattering process are governed by energy conservation and momentum conservation
ωs = ωi ± Ω (1)
ks = ki ± q (2)
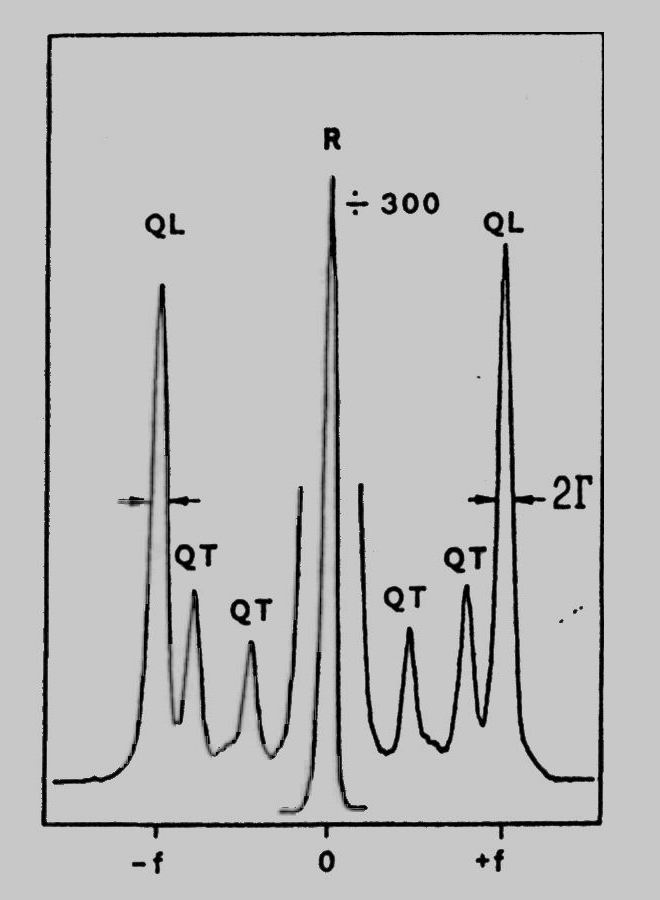
ωi /2π, ωs /2π and Ω /2π = f are the frequencies of the incident laser light, of the scattered light and of the involved sound wave respectively. ki and ks are the wave vectors of the Incident laser light and the scattered light with the sample, and q is the wave vector of the sound wave Involved. Within the scattering process phonons of energy hΩ are either created (ΩS = Ω-, Stokes scattering) or annihilated (ΩAS = Ω+, Anti-Stokes scattering). Generally, in solids three orthogonal polarized acoustic modes of different frequencies Ω (p, q) are related to each wave vector q (p = l, 2, 3) A typical BS spectrum of a solid is shown in fig. 1.
| Fig. 1 Brillouin spectrum (of Hexatriacontane at room temperature). The lines denoted by QL and QT represent the quasilongitudinal and quasitransverse acoustic phonons (seen as Stokes [-f] and anti-Stokes [+f] lines) at phonon frequency f. The quantity 2G measures the acoustic losses. R denotes the Rayleigh line which is due to elastic light scattering. For display purposes, the Rayleigh line has been reduced in height by a factor of 300 compared to the phonon lines. |
It consists of three pairs of Brillouin lines which are shifted away from the frequency wl of the exciting laser light by the frequency Ω(p) . The line width Γ(p, q) (half width at half maximum, HWHM) measures the temporal attenuation of the acoustic modes. Γ(p, q) is inversely proportional to the life time of the phonons Involved In the scattering process. For moderate sound attenuation (Γ(p, q) < Ω (p, q)) the sound velocity v(p, q) is related to the measured frequency Ω (p, q) by
v(p, q) = Ω (p, q) / q = f (p, q) Λ with p = 1, 2, 3 (3)
where Λ is the hypersonic wavelength.
The elastic stiffness coefficient is related to the sound velocity and the mass density of the material by
c (p, q) = ρ v2 (p, q) (4)
To account for energy dissipation effects complex quantities are chosen for the elastic stiffness coefficients [c*(p, q) = c’(p, q) - ic”(p, q)]. c*(p, q) Is related to the complex phonon frequency Ω*(p, q) = Ω’(p, q) - i Ω"(p, q) = Ω’(p, q) + i 2Γ(p, q) by:
Ω’(p, q) = Ω 0 [c’(p, q) / c(p, q)]1/2 = [q2 c’(p, q) /ρ]1/2 (5a)
with
Ω 0(p, q) = q [c(p, q) /ρ]1/2 (5b)
and
Ω"(p, q) = Γ(p, q) ≈ Ω’(p, q) [c”(p, q) / 2 c’(p, q)] (5c)
Eq. 5a and eq. 5b have been derived assuming that the elastic properties are independent of frequency. The Influence of dispersion on c’(p, q) and c"(p, q) is often small but can be taken into account in a formal way [4]. It should be noticed that in contrast to ultrasonic experiments where dispersion is reflected by the frequency dependence of the complex stiffness coefficient and in which the wave vector q(Ω) becomes the complex quantity, dispersion in Brillouin experiments is reflected by the variation of the elastic stiffness coefficient as a function of changes in magnitude of the wave vector. The consequences have been discussed by Evans et al. [5].
In isotropic solids the two transversely polarized sound modes degenerate and in neat, non-viscous (isotropic) liquids only the longitudinally polarized sound mode can propagate. For isotropic and cubic materials the following relation holds between the magnitude of the acoustic wave vector q = |q| and the scattering angle Φ = (ki ^ ks)
q = 2 ki sin(Φ /2) = (4πn/λ0) sin(Φ /2) (6)
where λ0 is the wave length of the laser light and n is the refractive index of the sample. The case of less symmetric systems becomes more complicated and is treated in section II.2 of the chapter.
References
[1] L. Brillouin, Ann. De Physique, 17, 88 (1922)
[2] L. I. Mandelshtam, Zh. Russ. Fiz. Khim. Obs., 58, 381 (1926)
[3] E. Gross, Nature, 126, 201,400,630 (1930)
[4] C. J. Montrose, V. A. Solovyev, T. A. Litivitz, J. Acoust. Soc. Am., 43,117 (1968)
[5] W. A. B. Evans, J. G. Powels. J. Phys. A, 7, 1944 (1974)