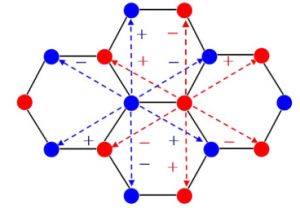
Symmetry Protected Topological (SPT) phases are kinds of zero temperature states of matter characterized by having a gap, some symmetry, and some topological invariant in such a way that any topological phase characterized by some value of the topological invariant is not smoothly connected to others with different invariants by any perturbation that preserves the symmetry unless a phase transition (gap closing and reopening) occurs. The transition can take place without closing the gap if the perturbation breaks the symmetry defining the SPT.
The non-trivial SPT states show gapless surface (edge) states that are protected against perturbations that respect the symmetry. Although these SPT phases can be bosonic or fermionic, the fermionic ones are the most studied ones in Condensed Matter Physics, being the topological band insulators the prototypical example.
Within this topic, our group has worked on the question of how interactions or disorder can help to stabilize (destabilize) these SPT fermionic phases. Since interactions can induce symmetry broken phases, according to the Landau theory of phase transitions, the question is if interactions can spontaneously break the symmetry protecting the SPT phases. Also, we ask the reciprocal question> for trivial SPT systems, could the interactions induce symmetry protected non/trivial phases?
The published works along these lines are:
[1] Topological Fermi Liquids from Coulomb Interactions in the Doped Honeycomb Lattice.
[3] Anomalous Hall metals from strong disorder in class A systems on bipartite lattices, arXiv:1601.07910, Journal-ref: Physical Review B 93, 245414 (2016);
[4] Anderson localization and topological transition in Chern insulators