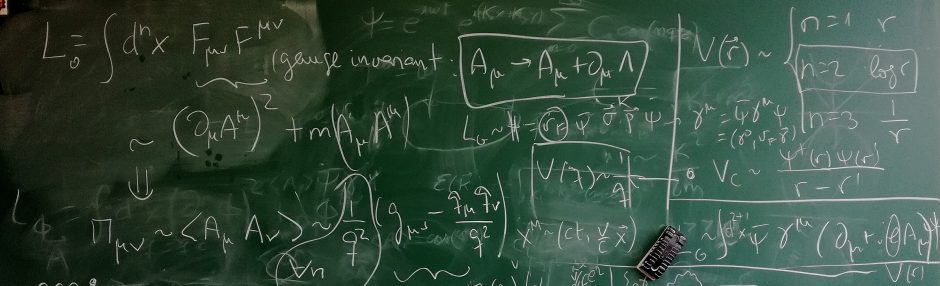I have been working in the frontier between quantum field theory and condensed matter for some time now. You can find a list of my publications in the arXiv au: Vozmediano.
Here I will select and comment on my favorite works – that do not coincide necesarily with the most cited or these published on higher impact journals-. I will follow a chronological order.
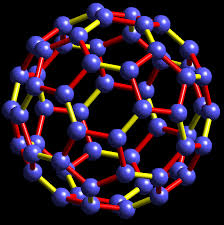
Lattice of the C60 molecule
- «Continuum approximation to fullerene molecules», J. Gonzalez, F. Guinea and A.H. Vozmediano, Phys. Rev. Lett. 69 (1992) 172. In this work, as early as 1992, we introduced the notion that curvature of the lattice would affect the electronic structure of a Dirac material coupling as a gauge field. The electronic structure of the C60 molecule was reproduced by solving the Dirac equation on the surface of a sphere with a magnetic monopole at its centre. This work has inspired all the later literature on strain and gauge fields. A summary of it up to 2010 can be seen in the review article «Gauge fields in graphene» arXiv:1003.5179
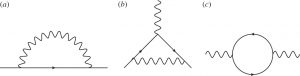
One loop Feynman graphs in QED
- «Non-Fermi liquid behavior of electrons in the half-lled honeycomb lattice. A Renormalization Group Approach», J. Gonzalez, F. Guinea y A.H. Vozmediano, Nucl.Phys. B424 (1994) 593. arXiv:hep-th/9311105. In this work, still published in a «Particles and fields» journal, we applied Renormalization Group techniques to analyze the Coulomb interactions in graphene (called sigle sheet of graphite in these times). We found the running upwards of the Fermi velocity as the energy is decreased, and the existence of a Lorentz invariant fixed point where the Fermi velocity equals the speed of light c. The prediction of the growth of the Fermi velocity was confirmed experimentally in 2011 (see the publication here: http://www.condmat.physics.manchester.ac.uk/pdf/mesoscopic/publications/graphene/SLGNatPhys2011.pdf). This work had a natural extension to Weyl semimetals recently worked out in 10.1103/PhysRevB.98.115122.
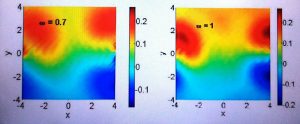
Correction to the local density of states in a wide region around two pairs of heptagon–pentagon defects located out of the region for increasing values of the energy.
- 1. Effects of topological defects and local curvature on the electronic properties of planar graphene, Alberto Cortijo, María A.H. Vozmediano, Nuclear Physics B 763 [FS] (2007) 293–308. arXiv:cond-mat/0612374 In this work we used a metric inspired on a cosmological problem (cosmic strings) to model topological defects in graphene (pentagon or heptagon rings). We also computed the density of states in real space. This is one of my favourite works together with its companions:
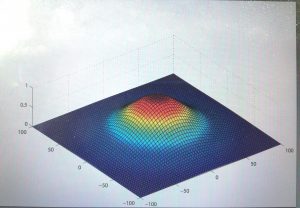
Gaussian bump in graphene
- 2. Charge inhomogeneities due to smooth ripples in graphene sheets, Fernando de Juan, Alberto Cortijo, and María A. H. Vozmediano, Phys. Rev. B 76, 165409 (2007), arXiv:0706.0176 where the gaussiam bump is introduced for the first time in graphene to model ripples with techniques of quantum field theory in curved space. This gaussian bump has later became a classic in the geometric modelling of curvature.
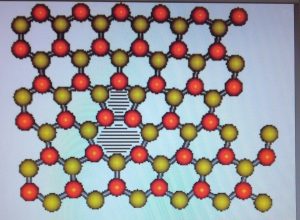
A glide dislocation in the Honeycomb lattice
- 3. Dislocations and torsion in graphene and related systems, Fernando de Juan, Alberto Cortijo, and María A. H. Vozmediano, Nucl. Phys. B 828, 625 (2010), arXiv:0909.4068. Pity that there are no screw dislocations in 2D systems. Still this is a very nice work with a good idea behind.
- Space dependent Fermi velocity in strained graphene Fernando de Juan, Mauricio Sturla, Maria A. H. Vozmediano, Phys. Rev. Lett. 108, 227205, (2012) arXiv:1201.2656. The dependence of the Fermi velocity on the position of the sample in corrugated samples is a prediction of the formalism of quantum field theory in curved space. In this work we generalize the tight binding expansion to obtain the result. This prediction was later experimentally confirmed. You can see the experiments here
arXiv:1209.1689 Observation of spatially-varying Fermi velocity in strained-graphene …
As an indirect consequence of this work we extracted in 10.1103/PhysRevB.88.155405 all possible electron-phonon couplings allowed by symmetries in graphene thanks to the deep knowledge of group theory of Juan Mañes. This very complete work has been later extended to 3D (more fun) Weyl semimetals with my student Vicente Arjona in 10.1103/PhysRevB.97.201404.
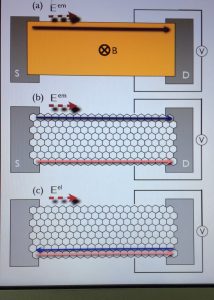
-
Topological electric current from time-dependent elastic deformations in graphene, Abolhassan Vaezi, Nima Abedpour, Reza Asgari, Alberto Cortijo, María A. H. Vozmediano, Phys. Rev. B 88, 125406, (2013), arXiv:1105.5232 This is a very original work starting with an idea from A. Vaezi where a piezo-electric response is described in gapped graphene (unfortunately BN was not there yet) coming from the mixed Chern–Simons action with the elastic and electromagnetic gauge fields.
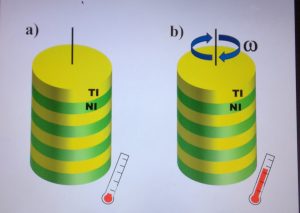
AME
- A condensed mater realization of the axial magnetic effect, Maxim Chernodub, Alberto Cortijo, Adolfo G. Grushin, Karl Landsteiner, María A. H. Vozmediano, Phys. Rev. B 89, 081407(R) (2014), arXiv:1311.0878. Weyl semimetals breaking time reversal symmetry have the two Weyl nodes separated in momentum space by a vector. In this work prior to the synthesis of the materials, we set up the idea that the nodes separation can be seen as an axial gauge field confined to the boundary of the sample. From this, in the presence of a temperature gradient, the axial magnetic effect, a high energy phenomenon associated to chiral matter, was postulated in the material. The temperature dependence was suggested as the first experimental evidence of the gravitational anomaly.
- The previous work started an joyful collaboration with the high energy colleagues that is giving rise to very original and interesting works as:
 Generation of a Nernst current from the conformal anomaly in Dirac and Weyl semimetals, Maxim Chernodub, Alberto Cortijo, and María A. H. Vozmediano, Phys. Rev. Lett. 120, 206601 (2018).arXiv:1712.05386. Interacting Dirac and Weyl semimetals are scale invariant at the classical level. The conformal anomaly gave rise to a «Scale magnetic effect» in an interesting paper by Maxim Chernodub «Anomalous Transport Due to the Conformal Anomaly» arXiv:1603.07993. We traded the gradient of the conformal factor by a temperature gradient using the ideas given in the cornerstone work by Luttinger on thermal transport coefficients: https://link.aps.org/doi/10.1103/PhysRev.135.A1505.
Generation of a Nernst current from the conformal anomaly in Dirac and Weyl semimetals, Maxim Chernodub, Alberto Cortijo, and María A. H. Vozmediano, Phys. Rev. Lett. 120, 206601 (2018).arXiv:1712.05386. Interacting Dirac and Weyl semimetals are scale invariant at the classical level. The conformal anomaly gave rise to a «Scale magnetic effect» in an interesting paper by Maxim Chernodub «Anomalous Transport Due to the Conformal Anomaly» arXiv:1603.07993. We traded the gradient of the conformal factor by a temperature gradient using the ideas given in the cornerstone work by Luttinger on thermal transport coefficients: https://link.aps.org/doi/10.1103/PhysRev.135.A1505.